C++ 關於某小數轉進制的題目-解題經驗

2141 words

11 minutes

C++ 關於某小數轉進制的題目-解題經驗

2019-10-11

C/C++

C++

/

小數

/

進制

/

演算法

前言#

最近我朋友問了我一個關於一個小數轉進制的題目，雖然我當時很忙，但最後我還是抽出了時間幫忙解決，解題的一開始我以為題目挺簡單的，但在解題過程發現還蠻多小技巧要使用，我會在這篇文章分享我的解題過程。

題目#

我先給各位看一下題目。

1
Objective
2

3
Programming using basic data types and control structures.
4

5
Specification
6

7
Write a program which converts a base-S floating point number with value in the range [0,1) to its equivalent base-D representation, where S, D =2, … , 10.
8

9
You program should be able to convert an input number with at least 8 significant digits而且.
10

11
Hint: Use input/output manipulators std::setw, std::setfill, and std::setprecision to format the output.
12

13
Sample run
14

15
Base conversion for numbers  [0,1)  with at least 8 significant digits.
16

17
Convert a number from base-S to base-D (2<=S<=10, 2<=D<=10):
18

19
Input S: 4
20

21
Input D: 9
22

23
Input a number [0,1)in base-4: 0.12341234
24

25
Error: 0.12341234 is an invalid base-4 number
26

27
Input a valid base-4 number: 0.12301230
28

29
0.12301230(4) is equivalent to 0.42352295(10) & 0.37266541(9)
30

31
Process another Conversion or Quit? (C/Q) C
32

33
Convert a number from base-S to base-D (2<=S<=10, 2<=D<=10):
34

35
Input S: 8
36

37
Input D: 5
38

39
Input a number in base-8: 0.66666666
40

41
0.66666666(8) is equivalent to 0.85714281(10) & 0.41203241(5)
42

43
Process another Conversion or Quit? (C/Q) Q
44

45
Note:
46

47
Ÿ  Download the grade sheet as the cover page of your homework report.
48

49
Ÿ  You may check the base converter for the assessment of your results.

題目理解#

這題目要我們先輸入我們想要轉換的進制，從 base-S 進制轉成 base-D 進制，接著要輸入一個至少小數點後有 8 位的小數，首先判斷該小數是否是否符合 base-S 的進制，如果不符合就重輸入，符合就轉進制，最後格式化分別輸出 10 進制與 base-D 進制的小數。

程序設計思路#

在決定小數的類型時，我們需要知道：
- float 類型的有效數字為 6 ~ 7 位
- double 有效數字 15 ~ 16 位
- long double 有效數字 18 ~ 19 位
根據題目要求至少輸入小數點後有 8 位有效數字，我們應該選擇 double 類型為我們的小數類型。
在全程使用 double 類型的變數存取小數時，會遇到數字精確度的問題，也就是在取小數位數時或是在轉換時數字的累加上，極有可能碰到數字尾部（有效數字外）出現了不知所然的位數，導致精確度不準確，也順帶影響運算結果。

為了避免這種情況，我們需要使用 String 類型來存取我們輸入的小數，以獲取我們輸入時的小數位數有多少，再利用位數使用循環將字符串轉成 double 類型，這一步我們主要就是小數位數，後面關於進制檢查與轉換都要用到小數位數。
在依序獲取小數每位數字時，可以先乘 10，再使用 (int) 強制轉換類型取得整數部份，將乘 10 的小數減去整數部份，持續循環。
題意不會要我們轉換 10 進制以上的小數（2 <= S <= 10, 2 <= D <= 10），這代表我們不需要擔心遇到英文字母，但遇到了其實也不麻煩，只要在轉換的地方添加字母條件去- 判斷是否為字母。
我們需要優先將小數轉成 10 進制，再轉成其他進制，這樣會有效讓我們去設計算法，如果是設計一個函式通用所有的轉制會很吃力。
從非 10 進制轉換到 10 進制的演算法，我們使用指數加權法：

註：來源參考 - 進制轉換 (二進制、八進制、十進制、十六進制) - NotFalse 技術客

e.g.

代碼實現

1
    int n = -1; // the power of n
2
    double base10 = 0; // copy convert1
3

4
    // Continuously taking decimal places
5
    // convert to base-10
6
    for(int i = 0; i < significant; i++)
7
    {
8
        number *= 10;
9
        *convert1 += (int)number * pow(S, n);
10
        // e.g. 1.1 (base-2) -> 1*2^0 + 1*2^(-1) = 1.5 (base-10)
11
        number -= (int)number;
12
        n -= 1;
13
    }

從 10 進制轉成非 10 進制的演算法，我們使用餘數乘積法：

註：來源參考 - 十进制小数转二进制小数方法

e.g.

代碼實現

1
    base10 = *convert1; // copy
2
    n = -1; // init
3
    // Continuously taking decimal places
4
    // convert base-10 to base-D
5
    /*
6
    Because the precision of double is 16 ,
7
    so multiply it by 17 and execute at least 17 times,
8
    otherwise it will enter an infinite loop.
9
     */
10
    for(int i = 0; i < 17; i++)
11
    {
12
        base10 *= D;
13

14
        *convert2 += (int)base10 * pow(10, n);
15
        base10 -= (int)base10;
16
        n -= 1;
17

18
        if(base10 == 0) // End early
19
        {
20
            break;
21
        }
22
    }

在輸出時使用 API 提供的函式格式化。

1
    cout << setiosflags(ios::fixed) << setprecision(8);

使用 GDB 進行調試，這樣能快速找到代碼問題。

Functions#

int main() ：主程序
double Scan(string, int *)：輸入 string 的小數，轉換成 double 類型，並計算輸入小數的小數位數
bool isValid(double, int, int)：判斷輸入的小數是否符合 base-S 進制
void convert(double, int, int, double *, double *, int)：先將小數轉成 10 進制，再轉成 base-D 進制

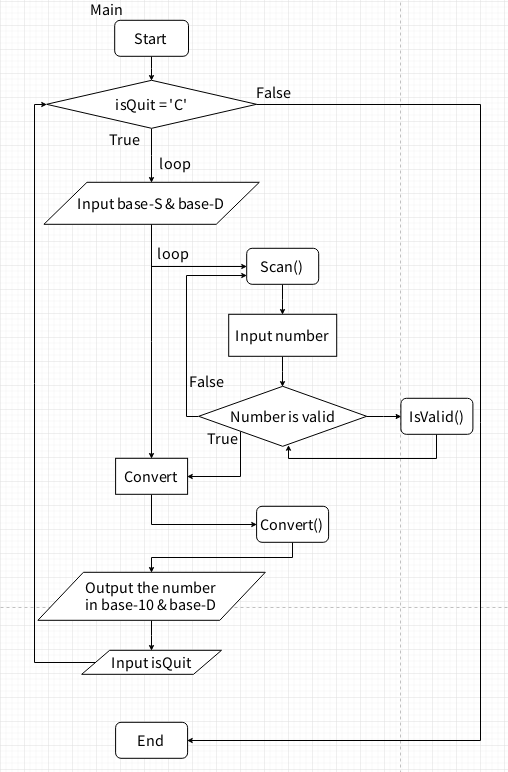
流程圖#

此圖為我設計的流程圖。

註：不知道為什麼我從 draw.io 導出的圖片在 linux 下會跑版，格式亂了╮(╯_╰)╭ 最後只好使用截圖工具

源代碼#

這裡還是強調一下，寫代碼時註解真的很重要，你的代碼不僅是要你自己可以快速釐清自己的代碼，不然一段時間後自己再看自己寫的內容又看不懂，而且要讓看你代碼的人能看懂。

1
#include<iostream>
2
#include<math.h>
3
#include<iomanip>
4
#include<string>
5
#include<stdlib.h>
6

7
using namespace std;
8

9
double Scan(string, int*); // count significant
10
bool isValid(double, int, int); // Judge the number's correctness (Base-S)
11
void convert(double, int, int, double *, double *, int); // convert the number from Base-S to Base-D and Base-10
12

13
int main()
14
{
15
    // initialize
16
    double number = 0; // The number we need to input
17
    int S = 0; // base-S
18
    int D = 0; // base-D
19
    char isQuit = 'C'; // Judge whether to leave
20
    double convert1 = 0, convert2 = 0; // the result from convert()
21
    string count; // The number we need to input
22
    int significant = 0; // the number's significant
23

24
    // loop, if isQuit's value is 'Q',break it.
25
    while(isQuit == 'C')
26
    {
27
        // description
28
        cout << "Base conversion for numbers  [0,1)  with at least 8 significant digits.\n";
29
        cout << "Convert a number from base-S to base-D (2<=S<=10, 2<=D<=10):\n";
30
        // input Base-S
31
        cout << "Input S: ";
32
        cin >> S;
33
        // input Base-D
34
        cout << "Input D: ";
35
        cin >> D;
36
        fflush(stdin);
37

38
        // loop
39
        while(1)
40
        {
41
            // input number
42
            cout << "Input a valid base-" << S << " number: ";
43
            // cin >> number;
44
            number = Scan(count, &significant);
45
            if(isValid(number, S, significant)) // number is valid
46
            {
47
                break;
48
            }
49
            else // number is invalid
50
            {
51
                cout << "Error: " << setiosflags(ios::fixed) << setprecision(8)
52
                 << number << " is an invalid base-" << S << " number\n";
53
            }
54
        }
55

56
        convert(number, S, D, &convert1, &convert2, significant); // convert
57

58
        // output the result
59
        cout << setiosflags(ios::fixed) << setprecision(8)
60
        << number << "(" << S <<") is equivalent to "
61
        << convert1 <<"(10) & "<< convert2 <<"("<< D << ")"<<endl;
62

63
        // input isQuit
64
        cout << "Process another Conversion or Quit? (C/Q) -> ";
65
        cin >> isQuit;
66
        // Letters into uppercase
67
        isQuit = toupper(isQuit);
68

69
        // initialize the values
70
        convert1 = 0;
71
        convert2 = 0;
72
        significant = 0;
73
    }
74
    system("pause");
75
    return 0;
76
}
77

78
double Scan(string count, int *significant)
79
{
80
    *significant = 0;
81
    double number = 0; // we need to enter
82
    int N = -1;
83

84
    cin >> count; // enter the string
85
    fflush(stdin);
86

87
    for(int i = 2; i < count.length(); i++) // use count's length to loop
88
    {
89
        *significant += 1; // count significant
90

91
        number += (count[i] - '0') * pow(10, N); // char -> double
92
        N -=1;
93
    }
94
    return number;
95
}
96

97
bool isValid(double number, int S, int significant)
98
{
99
    double swapDouble = 0;
100

101
    // Continuously taking decimal places
102
    for(int i = 0; i < significant; i++)
103
    {
104
        number *= 10;
105
        if((int)number >= S) // not meets Base-S
106
        {
107
            return false; // invalid
108
        }
109
        else
110
        {
111
            swapDouble = (double)((int)number);
112
            number -= swapDouble;
113
        }
114
    }
115
    return true; // valid
116
}
117

118
void convert(double number, int S, int D, double *convert1, double *convert2, int significant)
119
{
120
    int n = -1; // the power of n
121
    double base10 = 0; // copy convert1
122

123
    // Continuously taking decimal places
124
    // convert to base-10
125
    /*
126
    Reference
127
    https://notfalse.net/17/positional-numeral-systems-conversion
128
     */
129
    for(int i = 0; i < significant; i++)
130
    {
131
        number *= 10;
132
        *convert1 += (int)number * pow(S, n);
133
        // e.g. 1.1 (base-2) -> 1*2^0 + 1*2^(-1) = 1.5 (base-10)
134
        number -= (int)number;
135
        n -= 1;
136
    }
137
    base10 = *convert1; // copy
138
    n = -1; // init
139
    // Continuously taking decimal places
140
    // convert base-10 to base-D
141
    /*
142
    Because the precision of double is 16 ,
143
    so multiply it by 17 and execute at least 17 times,
144
    otherwise it will enter an infinite loop.
145

146
    Reference
147
    https://www.cnblogs.com/upzone/articles/1389365.html
148

149
     */
150
    for(int i = 0; i < 17; i++)
151
    {
152
        base10 *= D;
153

154
        *convert2 += (int)base10 * pow(10, n);
155
        base10 -= (int)base10;
156
        n -= 1;
157

158
        if(base10 == 0) // End early
159
        {
160
            break;
161
        }
162
    }
163
}